Kỹ thuật duyệt đồ thị (Graph traversal)

Phần này chúng ta thảo luận hai thuật toán đồ thị cơ bản: tìm kiếm theo chiều sâu (depth-first search) và tìm kiếm theo chiều rộng (breadth-first search). Cả hai thuật toán đều xuất phát tại một node trong đồ thị, và viếng thăm tất cả các node từ node bắt đầu. Sự khác nhau giữa hai thuật toán là thứ tự viếng thăm các nodes.

1. Tìm kiếm theo chiều sâu (Depth-first search)

Tìm kiếm theo chiều sâu (Depth-first search – DFS) là một kỹ thuật duyệt đồ thị cơ bản. Thuật toán bắt đầu tại một node, và tiếp tục đi đến các node khác từ node bắt đầu bằng các cạnh của đồ thị.

Tìm kiếm theo chiều sâu luôn theo một con đường duy nhất trong đồ thị để tìm các node mới. Sau đó, nó quay lại node liền trước và bắt đầu khai phá các con đường khác của đồ thị. Thuật toán lưu trữ các node đã viếng thăm, để nó đi đến mỗi node một lần duy nhất.

Ví dụ

Chúng ta xem xét cách tìm kiếm theo chiều sâu xử lý đồ thị sau:

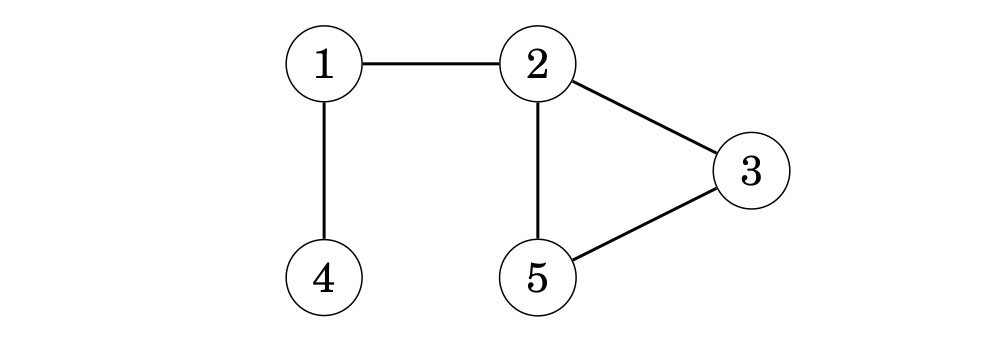
Chúng ta có thể bắt đầu tìm kiếm tại một node bất kỳ của đồ thị; bây giờ chúng ta bắt đầu việc tìm kiếm tại node 1.

Đầu tiên, việc tìm kiếm di chuyển đến node 2:

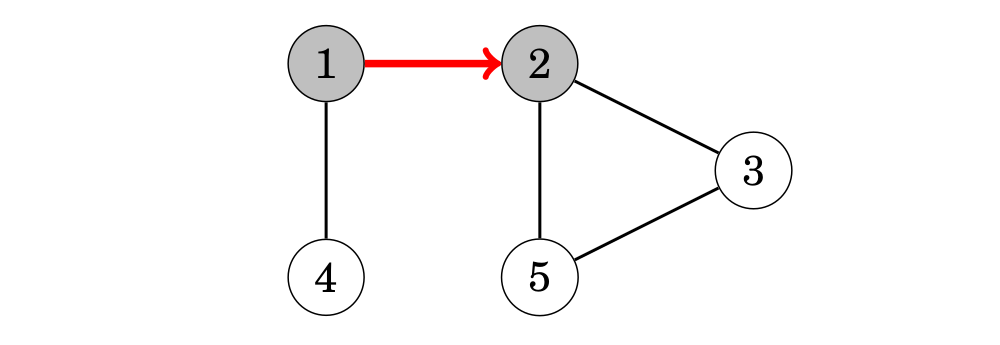
Sau đó, nodes 3 và 5 sẽ được viếng thăm:

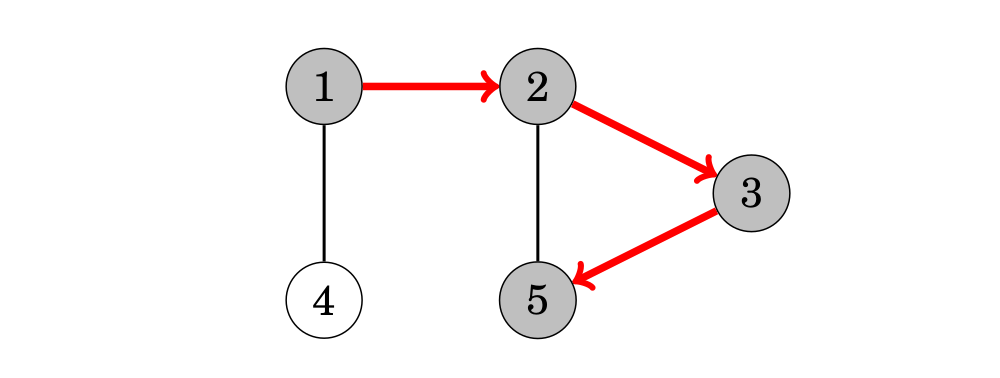
Các node kề của node 5 là 2 và 3, nhưng việc tìm kiếm đã vừa viếng thăm các nodes này, vì thế nó quay ngược lại các nodes trước đó. Cũng tương tự tất cả các nodes kề của 3 và 2 đều đã được viếng thăm, vì thế tiếp theo chúng ta di chuyển từ node 1 đến node 4.

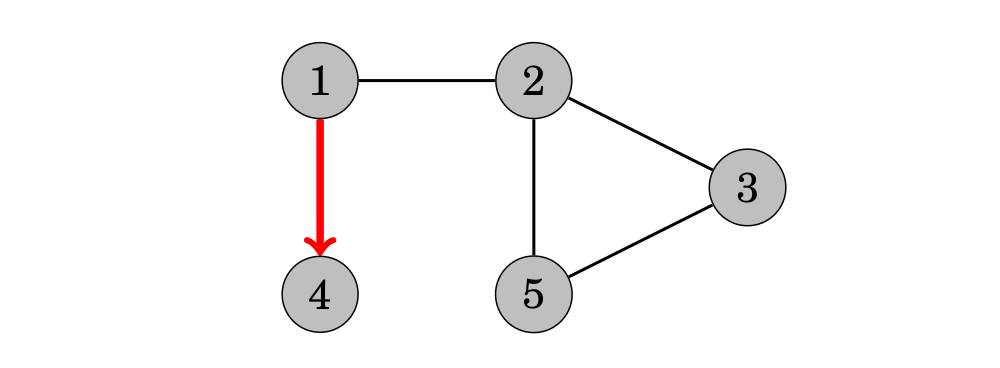
Sau đó, việc tìm kiếm kết thúc vì tất cả các nodes đã được viếng thăm.

Độ phức tạp thời gian của tìm kiếm theo chiều sâu là O(n + m) khi n là số lượng đỉnh và m là số lượng cạnh, vì thuật toán xử lý mỗi đỉnh và mỗi cạnh.

Thực thi mã

Tìm kiếm theo chiều sâu có thể được thực thi một cách tiện lợi bằng đệ quy. Hàm dfs sau bắt đầu một tìm kiếm theo chiều sâu tại một đỉnh xác định. Hàm giả thiết rằng đồ thị được lưu trữ theo danh sách kề trong một mảng:

vector<int> adj[N];

và cũng duy trì một mảng:

bool visited[N];

để lưu vết các đỉnh đã viếng thăm. Khởi tạo, mỗi giá trị của mảng là false, và khi việc tìm kiếm bắt đầu từ đỉnh s, giá trị của visited[s] thành true. Hàm có thể được thực thi như sau:

void dfs(s) {
	if (visited[s]) return;
	visited[s] = true;
	// process node s
	for(auto u : adj[s]) {
		dfs(u);
	}
}

2. Tìm kiếm theo chiều rộng (Breadth-first search)

Tìm kiếm theo chiều rộng (Breadth-first search – BFS) viếng thăm các đỉnh theo thứ tự tăng dần theo khoảng cách từ chúng đến đỉnh bắt đầu. Vì thế, chúng ta có thể tính toán khoảng cách từ đỉnh bắt đầu đến tất cả các đỉnh khác bằng tìm kiếm theo chiều rộng. Tuy nhiên, tìm kiếm theo chiều rộng thì khó thực thi hơn tìm kiếm theo chiều sâu.

Tìm kiếm theo chiều rộng đi qua các đỉnh cấp 1 sau đó mới đến các đỉnh khác. Đầu tiên, thuật toán tìm kiếm khai phá các đỉnh mà có khoảng cách đến đỉnh bắt đầu là 1, sau đó các đỉnh có khoảng cách là 2, v.v… Quá trình này được tiếp tục cho đến khi tất cả các đỉnh đã được viếng thăm.

Ví dụ

Chúng ta cùng xem xét cách tìm kiếm theo chiều rộng xử lý đồ thị sau:

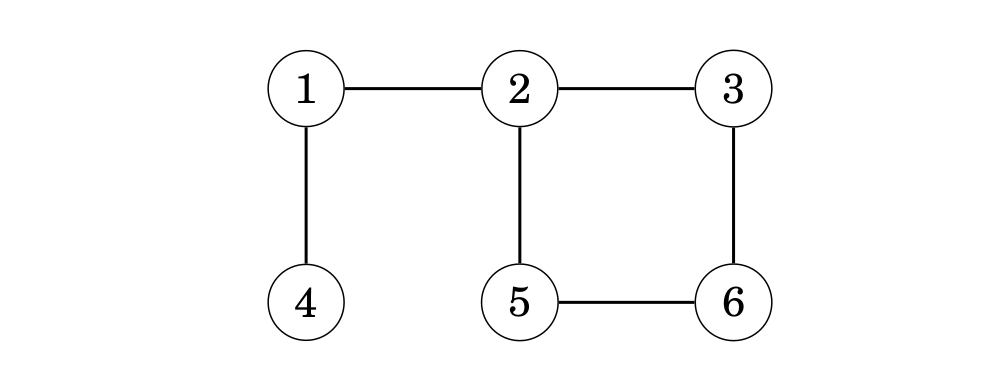
Giả thiết rằng việc tìm kiếm bắt đầu tại đỉnh 1. Đầu tiên, chúng ta xử lý tất cả các đỉnh có thể đi đến từ đỉnh 1 bằng một cạnh:

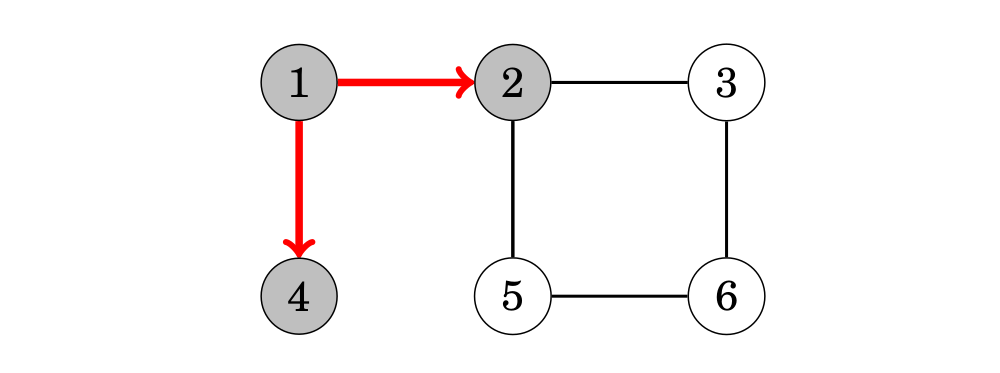
Sau đó, chúng ta di chuyển đến đỉnh 3 và 5:

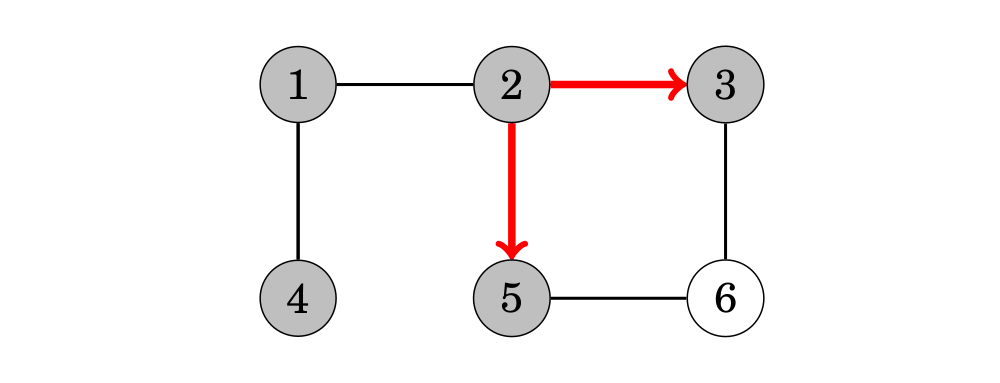
Cuối cùng, chúng ta thăm đỉnh 6:

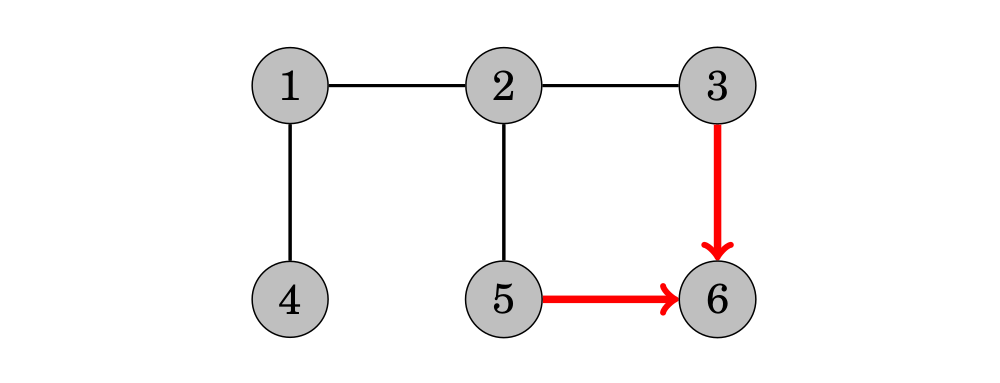
Bây giờ chúng ta tính toán khoảng cách từ đỉnh bắt đầu đến tất cả các đỉnh của đồ thị. Khoảng cách như sau:

Đỉnh 		Khoảng cách
1		0
2		1
3		2
4		1
5		2
6		3

Giống như tìm kiếm theo chiều sâu, độ phức tạp của tìm kiến theo chiều rộng là O(n + m), khi n là số lượng đỉnh và m là số lượng cạnh.

Thực thi mã

Tìm kiếm theo chiều rộng là khó thực thi mã hơn tìm kiếm theo chiều sâu, vì thuật toán viếng thăm các đỉnh trong nhiều đường khác nhau của đồ thị. Một thực thi điển hình là dựa trên một hàng đợi (queue) chứa các đỉnh. Tại mỗi bước, đỉnh tiếp theo trong hàng đợi sẽ được xử lý.

Mã sau giả thuyết rằng đồ thị được lưu trữ dạng danh sách kề và duy trì một cấu trúc dữ liệu như sau:

queue<int> q;
bool visited[N];
int distance[N];

Hàng đợi q chứa các đỉnh để xử lý theo thứ tự tăng dần khoảng cách của chúng. Các đỉnh mới luôn được thêm vào cuối hàng đợi, và một đỉnh tại đầu hàng đợi là đỉnh tiếp theo được xử lý. Mảng visited chỉ ra các đỉnh mà việc tìm kiếm đã viếng thăm, và mảng distance sẽ chứa khoảng cách từ đỉnh bắt đầu đến tất cả các đỉnh khác của đồ thị.

Việc tìm kiếm có thể được thực thi như sau, bắt đầu từ đỉnh x:

visited[x] = true;
distance[x] = 0;
q.push(x);
while(!q.empty()) {
	int s = q.front(); q.pop();
	// process node s
	for(auto u : adj[s]) {
		if(visited[u]) continue;
		visited[u] = true;
		distance[u] = distance[s] + 1;
		q.push(u);
	}
}

3. Ứng dụng (Applications)

Việc sử dụng các thuật toán duyệt đồ thị, chúng ta có thể kiểm tra nhiều thuộc tính của đồ thị. Thường, cả tìm kiếm theo chiều sâu và theo chiều rộng đều có thể được sử dụng, nhưng trong thực tế, tìm kiếm theo chiều sâu là lựa chọn tốt hơn, vì nó dễ thực thi hơn. Trong các ứng dụng sau, chúng ta sẽ giả thiết rằng đồ thị là vô hướng.

Kiểm tra tính liên thông (Connections check)

Một đồ thị là liên thông nếu có đường đi giữa 2 đỉnh bất kỳ thuộc đồ thị. Vì thế, chúng ta có thể kiểm tra nếu một đồ thị có liên thông bằng cách bắt đầu từ một đỉnh tùy ý và tìm kiếm xem ta có thể đi đến tất cả các đỉnh khác hay không. Ví dụ, trong đồ thị sau:

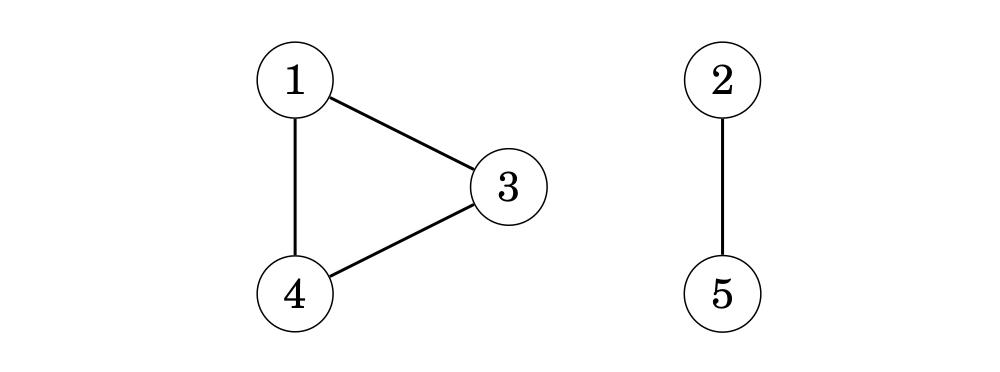
tìm kiếm theo chiều sâu từ đỉnh 1 viếng thăm các đỉnh như sau:

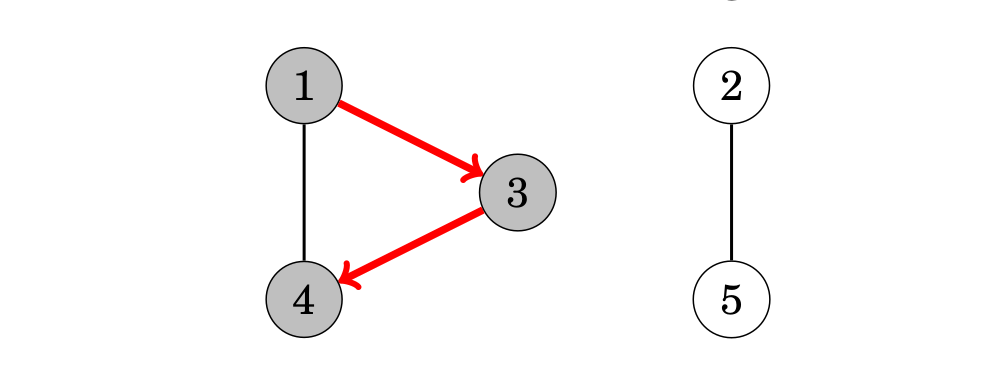
Khi việc tìm kiếm không thể viếng thăm tất cả các đỉnh, chúng ta kết luận rằng đồ thị là không liên thông. Trong cách tương tự, chúng ta có thể tìm tất các thành phần liên thông của đồ thị bằng cách duyệt qua các đỉnh và luôn bắt đầu một tìm kiếm theo chiều rộng mới nếu node hiện tại không thuộc về bất kỳ thành phần nào.

Tìm chu trình (Finding cycles)

Một đồ thị chứa một chu trình nếu trong suốt quá trình duyệt đồ thị, chúng ta tìm được một đỉnh mà tất cả đỉnh kề (những đỉnh khác ngoài các đỉnh trước đó trong con đường) đều đã được viếng thăm. Ví dụ, đồ thị

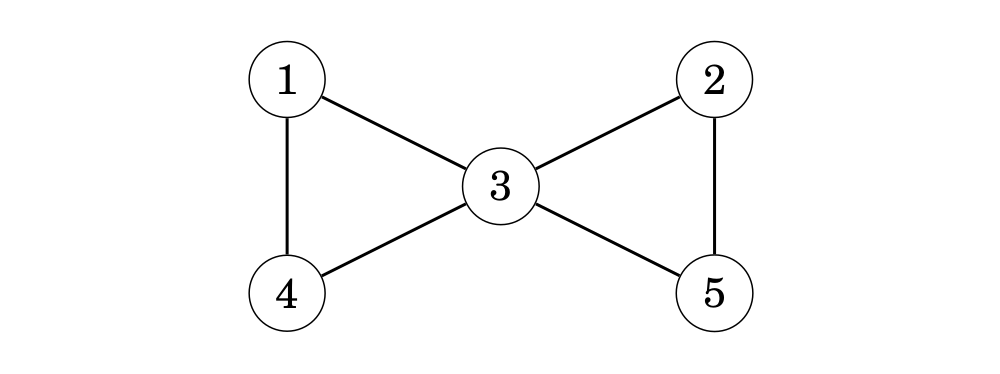
chứa 2 chu trình và chúng ta có thể tìm một trong số chúng như sau:

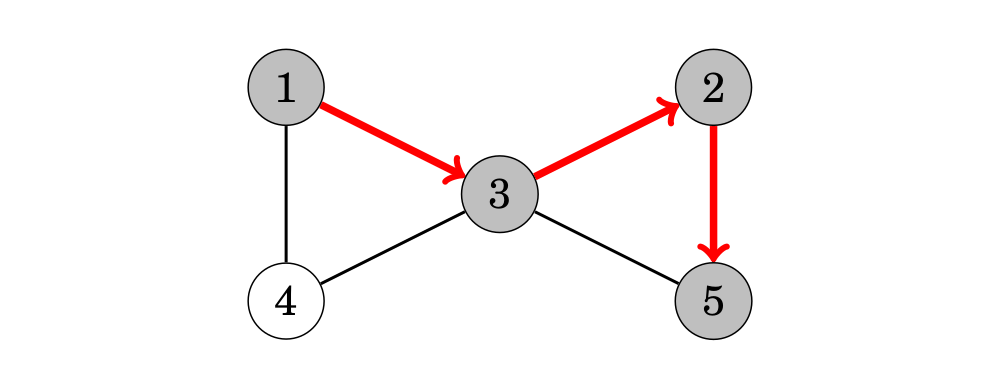
Sau khi đi từ đỉnh 2 sang đỉnh 5, chúng ta chú ý rằng các đỉnh kề của 3 và 5 đều đã được viếng thăm. Vì thế, đồ thị chứa một chu trình đi qua đỉnh 3, ví dụ, 3 → 2 → 5 → 3.

Một cách khác để tìm xem đồ thị có chứa chu trình hay không, thì đơn giản chỉ cần tính số lượng đỉnh và cạnh trong mỗi thành phần. Nếu thành phần chứa c đỉnh và không có chu trình thì nó phải có chính xác c -1 cạnh (vì nó trở thành cây tree). Nếu có c hoặc nhiều cạnh hơn thì thành phần chắc chắn chứa một chu trình.

Kiểm tra đồ thị phân đôi (Bipartiteness check)

Một đồ thị là đồ thị phân đôi nếu các đỉnh của nó có thể được tô bằng 2 màu sao cho không có đỉnh kề nào có cùng màu. Một cách đơn giản để kiểm tra xem đồ thị có là đồ thị phân đôi, ta dùng các thuật toán duyệt đồ thị.

Ý tưởng là tô màu đỉnh bắt đầu màu xanh, tất cả các đỉnh kề của nó màu đỏ, tất cả các đỉnh kề của những đỉnh này là màu xanh, và v.v… Nếu trong quá trình tìm kiếm, chúng ta thấy rằng 2 đỉnh kề nhau có cùng 1 màu, điều này có nghĩa rằng đồ thị không là đồ thị phân đôi. Ngược lại, đồ thị là đồ thị phân đôi và một cách tô màu được tìm thấy. Ví dụ, đồ thị

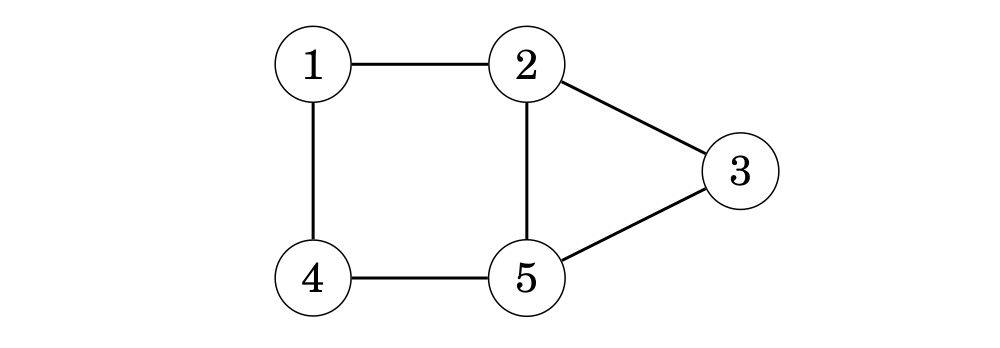
không là đồ thị phân đôi, vì quá trình tìm kiếm từ đỉnh 1 dẫn đến như sau:

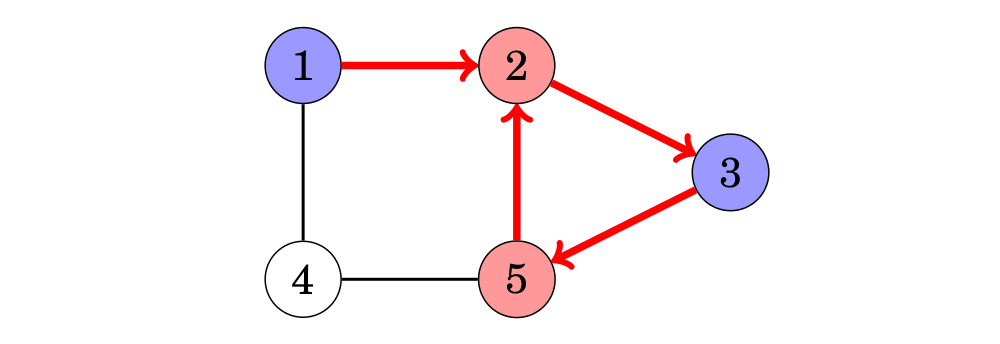
Chúng ta chú ý rằng màu sắc của đỉnh 2 và 5 đều là màu đỏ, trong khi chúng là 2 đỉnh kề nhau trong đồ thị. Vì thế, đồ thị không là đồ thị phân đôi.

Thuật toán này luôn làm việc, vì khi chỉ có 2 màu, thì việc tô màu đỉnh bắt đầu trong một thành phần, xác định màu sắc của tất cả các đỉnh khác trong thành phần này. Không có sự khác nhau nào nếu đỉnh bắt đầu được tô màu đỏ hay xanh.

Chú ý rằng, trong trường hợp tổng quát, thật khó để tìm xem các đỉnh trong đồ thị có thể được tô bằng k màu, sao cho các đỉnh kề không cùng màu. Thậm chí khi k = 3, cũng không có thuật toán nào giải quyết hiệu quả vì bài toán có độ khó NP-hard.