1. Thuật Toán Tìm Kiếm Là Gì
Tìm kiếm là quá trình tìm một phần tử nằm trong một tập hợp nhiều phần tử dựa vào một miêu tả nào đó. Ví dụ bạn cần tìm đồng 10k trong một đống tiền từ 10k đến 100k thì quá trình đó ta gọi là tìm kiếm.
Nếu một tập hợp đã được sắp xếp thì quá trình tìm kiếm trong tập hợp đó sẽ nhanh hơn. Ở thí dụ trên nếu đống tiền từ 10k đến 100k đã được sắp xếp tăng dần hoặc giảm dần thì ta cực kỳ dễ dàng tìm kiếm tờ 10k. Nhưng nếu đó là 1 đống tiền lộn xộn thì bạn sẽ mất nhiều thời gian để xử lý chúng.
Vậy thuật toán tìm kiếm là thuật toán dùng để kiếm tìm phần tử trong 1 danh sách cho trước theo một tiêu chí nhất định. Chúng ta thường sử dụng hai thuật toán đó là thuật toán tìm kiếm tuyến tính và thuật toán tìm kiếm nhị phần.
Thuật toán tìm kiếm tuyến tính là quá trình tìm kiếm trong một tập hợp chưa sắp xếp, giống với đống tiền chưa được sắp xếp ở ví dụ trên. Còn thuật toán tìm kiếm nhị phân là quá trình tìm kiếm trong một dãy đã được sắp xếp. Cả hai thuật toán đều có những ưu và nhược điểm khác nhau.
2. Các Thuật Toán Tìm Kiếm Trong C++
Trong bài viết này, mình sẽ giới thiệu đến các bạn các thuật toán tìm kiếm trong C ++ phổ biến nhất. Giờ hãy bắt đầu tìm hiểu về các thuật toán tìm kiếm này nhé!
+ Thuật Toán Tìm Kiếm Tuyến Tính
Thuật toán tìm kiếm tuyến tính (linear search) hay còn gọi là thuật toán tìm kiếm tuần tự (Sequential search) là một phương pháp tìm kiếm một phần tử cho trước trong một danh sách bằng cách duyệt lần lượt từng phần tử của danh sách đó cho đến lúc tìm thấy giá trị mong muốn hay đã duyệt qua toàn bộ danh sách.
Tìm kiếm tuyến tính là một giải thuật rất đơn giản khi hiện thực. Giải thuật này tỏ ra khá hiệu quả khi cần tìm kiếm trên một danh sách đủ nhỏ hoặc một danh sách chưa sắp thứ tự đơn giản. Trong trường hợp cần tìm kiếm nhiều lần, dữ liệu thường được xử lý một lần trước khi tìm kiếm: có thể được sắp xếp theo thứ tự, hoặc được xây dựng theo một cấu trúc dữ liệu đặc trưng cho giải thuật hiệu quả hơn,…
Bài toán: Cho một mảng mảng [] gồm n phần tử, hãy viết hàm để tìm kiếm một phần tử x đã cho trong mảng [].
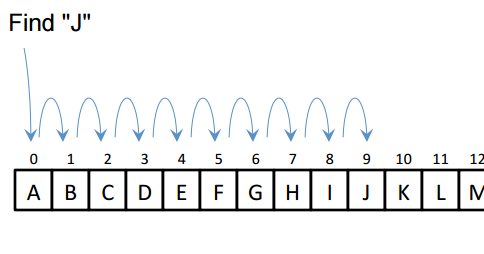
Ví dụ:
Đầu vào: mảng A[] = {10, 20, 80, 30, 60, 50,
110, 100, 130, 170}
x = 110;
Đầu ra: 6
Phần tử x có mặt ở vị trí số 6
Đầu vào: mảng A[] = {10, 20, 80, 30, 60, 50,
110, 100, 130, 170}
x = 175;
Đầu ra: -1
Phần tử x không có trong mảng A[].Mã giả
Phiên bản lặp tự nhiên
Đây là phiên bản hay gặp nhất của giải thuật này, kết quả trả về sẽ là vị trí của phần tử cần tìm hoặc một giá trị Δ thể hiện việc không tìm thấy phần tử trong danh sách đó.
1. For each item in the list:
1. if that item has the desired value,
1. stop the search and return the item's location.
2. Return 'Δ'Nếu danh sách được lưu trữ dưới dạng mảng, vị trí của phần tử cần tìm có thể là chỉ số của nó trong mảng, còn giá trị Δ có thể là chỉ số nằm trước phần tử đầu tien (0 hoặc -1 tùy vào danh sách).
Nếu danh sách là một danh sách liên kết, vị trí của phần tử được trả về có thể nằm dưới dạng địa chỉ của no, còn giá trị Δ có thể là giá trị null.
Phiên bản đệ quy
Đây là phiên bản đệ quy khi hiện thực giải thuật tìm kiếm tuần tự.
1. if the list is empty, return Λ;
2. else
1. if the first item of the list has the desired value
1. return its location;
2. else
1. search the value in the remainder of the list, and return the result.Sử dụng phần tử cầm canh
Một phương pháp được sử dụng để cải thiện hiệu quả của giải thuật là chèn phần tử muốn tìm kiếm và cuối danh sách như một phần tử cầm canh (sentinel) như được trình bày dưới đây:\
1. Set A[n + 1] to x.
2. Set i to 1.
3. Repeat this loop:
1. If A[i] = x,
1. exit the loop.
2. Set i to i + 1.
4. Return i.Việc thêm phần tử cầm canh giúp giảm bớt việc so sánh chỉ số hiện tại i với số các phần tử n ở mỗi vòng lặp. Tuy nhiên, điều này chỉ có thể được sử dụng khi vị trí cuối cùng của danh sách tồn tại nhưng chưa được sử dụng.
Viết thuật toán tìm kiếm tuyến tính với ngôn ngữ lập trình C, C++, Java, Python3
Tìm kiếm tuyến tính với C++:
#include <iostream>
using namespace std;
int search(int arr[], int n, int x)
{
int i;
for (i = 0; i < n; i++)
if (arr[i] == x)
return i;
return -1;
}
int main(void)
{
int arr[] = { 2, 3, 4, 10, 40 };
int x = 10;
int n = sizeof(arr) / sizeof(arr[0]);
int result = search(arr, n, x);
(result == -1)? cout<<"Element is not present in array"
: cout<<"Element is present at index " <<result;
return 0;
}Tìm kiếm tuyến tính với C:
#include <stdio.h>
int search(int arr[], int n, int x)
{
int i;
for (i = 0; i < n; i++)
if (arr[i] == x)
return i;
return -1;
}
int main(void)
{
int arr[] = { 2, 3, 4, 10, 40 };
int x = 10;
int n = sizeof(arr) / sizeof(arr[0]);
int result = search(arr, n, x);
(result == -1) ? printf("Element is not present in array")
: printf("Element is present at index %d",
result);
return 0;
}Tìm kiếm tuyến tính với Python3:
def search(arr, n, x):
for i in range (0, n):
if (arr[i] == x):
return i;
return -1;
# Driver Code
arr = [ 2, 3, 4, 10, 40 ];
x = 10;
n = len(arr);
result = search(arr, n, x)
if(result == -1):
print("Element is not present in array")
else:
print("Element is present at index", result);Tìm kiếm tuyến tính với Java:
class GFG
{
public static int search(int arr[], int x)
{
int n = arr.length;
for(int i = 0; i < n; i++)
{
if(arr[i] == x)
return i;
}
return -1;
}
public static void main(String args[])
{
int arr[] = { 2, 3, 4, 10, 40 };
int x = 10;
int result = search(arr, x);
if(result == -1)
System.out.print("Element is not present in array");
else
System.out.print("Element is present at index " + result);
}
}Tìm kiếm tuyến tính với PHP:
<?php
function search($arr, $x)
{
$n = sizeof($arr);
for($i = 0; $i < $n; $i++)
{
if($arr[$i] == $x)
return $i;
}
return -1;
}
// Driver Code
$arr = array(2, 3, 4, 10, 40);
$x = 10;
$result = search($arr, $x);
if($result == -1)
echo "Element is not present in array";
else
echo "Element is present at index " ,
$result;
?>Tìm kiếm tuyến tính với C#:
using System;
class GFG
{
public static int search(int[] arr, int x)
{
int n = arr.Length;
for(int i = 0; i < n; i++)
{
if(arr[i] == x)
return i;
}
return -1;
}
public static void Main()
{
int[] arr = { 2, 3, 4, 10, 40 };
int x = 10;
int result = search(arr, x);
if(result == -1)
Console.WriteLine("Element is not present in array");
else
Console.WriteLine("Element is present at index "+ result);
}
}Chạy thử và xem kết quả:
Element is present at index 3+ Thuật Toán Tìm Kiếm Nhị Phân
Thuật toán tìm kiếm nhị phân là một trong các thuật toán sắp xếp được sử dụng rất nhiều trong thực tế. Hãy cùng mình đi tìm hiểu thuật toán tìm kiếm này nhé.
Tìm kiếm là một phần không thể thiếu của mọi ứng dụng, website hay phần mềm. Tính năng tìm kiếm cho phép người sử dụng nhanh chóng truy vấn và tìm kiếm các bản ghi theo mong muốn. Và một công cụ tìm kiếm nổi tiếng nhất hàng ngày chúng ta vẫn thường sử dụng đó là Google search.
Bài viết ngày hôm nay Techacademy sẽ giới thiệu cho độc giả một thuật toán tìm kiếm tối ưu áp dụng đối với trường hợp dữ liệu số đã sắp xếp.
Phát biểu thuật toán tìm kiếm nhị phân(Binary search)
Cho một mảng đã sắp xếp arr[] có n phần tử, viết một hàm tìm kiếm trả về chỉ số của phần tử có giá trị x trong arr[].
Giải thuật đơn giản nhất cho bài toán này là sử dụng linear search(tìm kiếm tuyến tính). Tức là bạn sẽ phải đi qua từng phần tử của mảng để đối chiếu với x cần tìm. Thuật toán này trong trường hợp xấu nhất cho độ phức tạp là O(n). Mình cũng sẽ minh họa code của thuật toán này dưới đây.
Đây là code C/C++ sử dụng linear search.
// Code from https://techacademy.edu.vn
#include <stdio.h>
int search(int arr[], int n, int x)
{
int i;
for (i = 0; i < n; i++)
if (arr[i] == x)
// Trả về chỉ số khi tìm thấy
return i;
// Nếu không tìm thấy trả về -1. Vì chỉ số mảng >= 0
return -1;
}
int main() {
int arr[] = {2, 3, 4, 10, 40};
int n = sizeof(arr) / sizeof(arr[0]);
int x = 10;
int result = search(arr, n, x);
if (result != -1) {
printf("%d xuat hien tai chi so %d", x, result);
} else {
printf("%d khong co trong mang", x);
}
return 0;
}Ý tưởng của thuật toán tìm kiếm nhị phân
Chú ý: Trong bài viết tôi giả sử mảng đang sắp xếp tăng dần. Với trường hợp mảng sắp xếp giảm dần, bạn đọc sau khi hiểu thuật toán sẽ có thể tự làm.
Do tính chất mảng đã sắp xếp, công việc tìm kiếm phần tử x có thể triển khai như sau:
- Xét đoạn mảng arr[left…right] cần tìm kiếm phần tử x. Ta so sánh x với phần tử ở vị trí giữa của mảng(mid = (left + right)/2). Nếu:
- Nếu phần tử arr[mid] = x. Kết luận và thoát chương trình.
- Nếu arr[mid] < x. Chỉ thực hiện tìm kiếm trên đoạn arr[mid+1…right].
- Nếu arr[mid] > x. Chỉ thực hiện tìm kiếm trên đoạn arr[left…mid-1].
Bằng cách áp dụng thuật toán tìm kiếm nhị phân, độ phức tạp cho trường hợp xấu nhất là O(log(n)).
Minh họa code cho thuật toán tìm kiếm nhị phân
Trong phần này, mình sẽ minh họa code sử dụng giải thuật đệ quy dùng Java và C/C++. Ngoài ra, tôi sẽ áp dụng thêm giải thuật khử đệ quy với C/C++.
Code minh họa C/C++ sử dụng đệ quy
// Code from https://nguyenvanhieu.vn
#include <stdio.h>
// Hàm tìm kiếm nhị phân sử dụng giải thuật đệ quy
int binarySearch(int arr[], int l, int r, int x) {
if (r >= l) {
int mid = l + (r - l) / 2; // Tương đương (l+r)/2 nhưng ưu điểm tránh tràn số khi l,r lớn
// Nếu arr[mid] = x, trả về chỉ số và kết thúc.
if (arr[mid] == x)
return mid;
// Nếu arr[mid] > x, thực hiện tìm kiếm nửa trái của mảng
if (arr[mid] > x)
return binarySearch(arr, l, mid - 1, x);
// Nếu arr[mid] < x, thực hiện tìm kiếm nửa phải của mảng
return binarySearch(arr, mid + 1, r, x);
}
// Nếu không tìm thấy
return -1;
}
int main(void) {
int arr[] = {2, 3, 4, 10, 40};
int n = sizeof(arr) / sizeof(arr[0]);
int x = 10;
int result = binarySearch(arr, 0, n - 1, x);
if (result == -1)
printf("%d xuat hien tai chi so %d", x, result);
else
printf("%d xuat hien tai chi so %d", x, result);
return 0;
}Code minh họa sử dụng đệ quy Java
// Code from https://nguyenvanhieu.vn
class BinarySearch {
int binarySearch(int arr[], int l, int r, int x) {
if (r >= l) {
int mid = l + (r - l) / 2;
// Nếu arr[mid] = x, trả về chỉ số và kết thúc
if (arr[mid] == x)
return mid;
// Nếu arr[mid] > x, gọi đệ quy tìm kiếm bên trái
if (arr[mid] > x)
return binarySearch(arr, l, mid - 1, x);
// Ngược lại, nếu arr[mid] < x, gọi đệ quy tìm kiếm bên phải
return binarySearch(arr, mid + 1, r, x);
}
// Trong trường hợp không tìm thấy
return -1;
}
public static void main(String args[]) {
BinarySearch ob = new BinarySearch();
int arr[] = {2, 3, 4, 10, 40};
int n = arr.length;
int x = 10;
int result = ob.binarySearch(arr, 0, n - 1, x);
if (result == -1)
System.out.println("Không tìm thấy phần tử " + x);
else
System.out.println("Phần tử " + x + " được tìm thấy tại chỉ số " +
result);
}
}Code khử đệ quy sử dụng C/C++
// Code from https://nguyenvanhieu.vn
#include <stdio.h>
// Hàm tìm kiếm nhị phân sử dụng giải thuật đệ quy
int binarySearch(int arr[], int n, int x) {
int r = n - 1; // chỉ số phần tử cuối
int l = 0; // Chỉ số phần tử đầu tiên
while (r >= l) {
int mid = l + (r - l) / 2; // Tương đương (l+r)/2 nhưng ưu điểm tránh tràn số khi l,r lớn
// Nếu arr[mid] = x, trả về chỉ số và kết thúc.
if (arr[mid] == x)
return mid;
// Nếu arr[mid] > x, cập nhật lại right
if (arr[mid] > x)
r = mid - 1;
// Nếu arr[mid] < x, cập nhật lại left
if (arr[mid] < x)
l = mid + 1;
}
// Nếu không tìm thấy
return -1;
}
int main(void) {
int arr[] = {
2,
3,
4,
10,
40
};
int n = sizeof(arr) / sizeof(arr[0]);
int x = 10;
int result = binarySearch(arr, n, x);
if (result == -1)
printf("%d xuat hien tai chi so %d", x, result);
else
printf("%d xuat hien tai chi so %d", x, result);
return 0;
}+ Thuật Toán Tìm Kiếm Nội Suy
Thuật toán tìm kiếm nội suy là một sự cải tiến của tìm kiếm nhị phân Binary Search. Nó có xu hướng tiến gần đến vị trí, giá trị tìm kiếm. Do đó tốc độ tìm kiếm được tối ưu rất cao và nhanh hơn nhiều so với Binary Search.
Cách thức hoạt động của nó dựa trên Binary Search, nhưng có sự cải tiến hơn. Đó chính là nó tìm ra phần tử gần với giá trị tìm kiếm nhất và bắt đầu từ đó để tìm.
Ví dụ:
Chúng ta có danh sách các sinh viên trong một lớp. Nếu chúng ta muốn tìm một bạn tên Tiến, thì chúng ta sẽ ưu tiên việc tìm kiếm từ cuối danh sách. Chứ không nên tìm kiếm từ đầu danh sách vì điều đó rất mất thời gian.
Với Interpolation Search nó sẽ linh hoạt hơn rất nhiều trong lúc tìm kiếm
Giả xử chúng ta có:
- Left, right là hai vị trí đầu và cuối.
- T là tập.
- X là giá trị cần tìm.
Giải thích thuật toán
Bước 1:Chúng ta sẽ sử dụng công thức tìm phần tử chính giữa của tập theo cách tìm kiếm Binary Search:
Search = left + (right - left) * 1/2Trong công thức trên chúng ta sẽ thay giá trị 1/2 bằng biểu thức sau:
(X - T[left]) / (T[right] - T[left])Sau khi thay biểu thức vào công thức sẽ được công thức mới như sau:
Search = left + (X- T[left]) * (right – left) / (T[right] – T[left])Bước 2: Bây giờ chúng ta sẽ kiểm tra T[Search] nếu bằng X thì Search chính là vị trí cần tìm.
- Nếu Search < X thì tăng left lên một đơn vị rồi quay lại bước 1.
- Nếu Search > X thì giảm right xuống một đơn vị rồi quay lại bước 1.
Thuật toán tìm kiếm Interpolation Search
int InterPolationSearch(int arr[], int n, int x)
{
int left = 0;
int right = n-1;
while (left <= right && x >= arr[left] && x <= arr[right])
{
double val1 = (double) (x - arr[left]) / (arr[right]-arr[left]);
int val2 = (right-left);
int Search = left + val1*val2;
if (arr[Search] == x)
return Search;
if (arr[Search] < x)
left = Search + 1;
else
right = Search - 1;
}
return -1;
}+ Thuật Toán Ternary Search
Tương tự với thuật toán tìm kiếm nhị phân, Ternary Search – Tìm kiếm tam phân là một kỹ thuật trong khoa học máy tính dùng để tìm kiếm giá trị lớn nhất (maximum) hay nhỏ nhất (minimum) của một unimodal function, và đây cũng là một ví dụ ứng dụng lớp thuật toán Chia để trị (divide and conquer).
Độ phức tạp thời gian: O (log [n]) trong đó cơ số của log = 3
Độ phức tạp của không gian: O (1) để thực hiện lặp lại trong khi O (log [n]) để thực hiện đệ quy
Ví dụ:
#include<iostream>
using namespace std;
int ternaryI(int a[], int target, int n)
{
int l = 0;
int r = n-1;
while( r-l>=0 ) {
int partiton = (r-l)/3;
int mid1 = l + partiton;
int mid2 = r - partiton;
if ( target == a[mid1])
return mid1;
else if ( target == a[mid2])
return mid2;
else if ( target < a[mid1] )
r = mid1-1;
else if ( target > a[mid2] )
l = mid2+1;
else {
l = mid1+1;
r = mid2-1;
}
} // while ends
return -1;
} // function ends
int main()
{
int arr[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
int n = 10;
int target = 7;
int tsi = ternaryI(arr, target, n);
cout << "Result of TSI = " << tsi << endl;
return 0;
} // main ends+ Thuật Toán Jump Search
Bài hôm nay chúng ta cùng tìm hiểu về thuật toán Jump Search (Thuật toán tìm kiếm nhảy)
Nguyên lý cơ bản của Jump Search
Cũng giống như giải thuật Binary Search. Jump Search cũng yêu cầu danh sách đã cho phải là một danh sách đã được sắp xếp theo thứ tự đã biết.
Ví dụ là tăng dần.
Cơ chế của Jump Search đó là tìm ra một hệ số nhảy được tính bằng : Căn bậc hai của số phần tử.
Từ hệ số tìm được, Jump Search sẽ thực hiện nhảy phần tử theo hệ số để tìm ra phần từ lớn hơn giá trị tìm kiếm.
=> Phần tử tìm kiếm sẽ nằm trong khoảng của nhảy mà chứa phần từ lớn hơn giá trị tìm kiếm ở trên.
Minh Họa hình vẽ như sau:
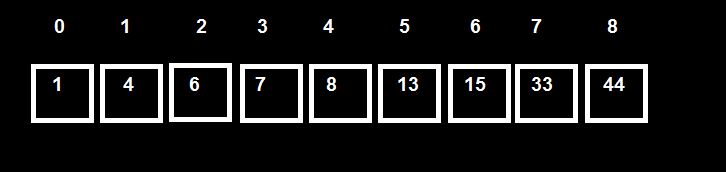
Tôi có tập 9 phần từ đã được sắp xếp theo thứ tự tăng dần.
Tôi xác định giá trị nhảy là step = √9 = 3 .
Giả sử giá trị cần tìm là 33.
Sử dụng một biến prev để lưu vị trí bắt đầu.
Một biến jump để nhảy.
Step 1:
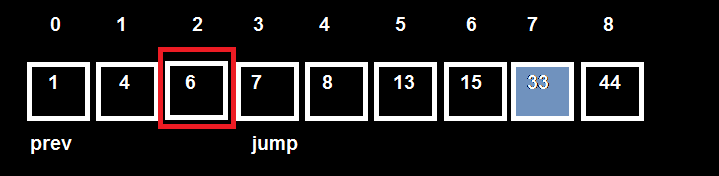
Gán prev = jump = 6
Nhảy jump = jump + step = 9 (bằng số phần tử, nếu jum lớn hơn n thì gán jum = n)
Lại kiểm tra T[jump – 1] => T[8] = 44 > 33 => Đã tìm được khoảng chứa giá trị cần tìm.
Khoảng chứa giá trị cần tìm là từ prev = 6 , jump = 9.
Lúc này chúng ta chỉ việc kiểm tra tuyến tính tệp từ vị trí prev đến jump để tìm ra giá trị cần tìm.
Sử dụng for hoặc while để duyệt phần tử trong khoảng prev – jump.
Các tính chất thuật toán.
– Tập cần tìm kiếm là phải được xắp xếp trước và biết rõ theo chiều tăng giảm.
– ĐỘ PHỨC TẠP HAY THỜI GIAN THỰC THI CỦA THUẬT TOÁN LÀ: O = √(n)
Thực hành Jump Search
Bây giờ từ nguyên lý ở trên chúng ta sẽ cùng thực hành với code c++
Hàm JumpSearch
// Techacademy.edu.vn
#include <iostream>
#include <conio.h>
#include <math.h>
int JumpSearch(int arr[], const int& n, const int& x)
{
int step = sqrt(1.0*n);
int prev = 0;
int jump = step;
//Find element > x
while(arr[jump - 1] < x)
{
prev = jump;
jump += step;
if (jump > n)
jump = n;
if (prev > n)
return -1;
}
// When found element > x.
while(arr[prev] < x)
{
prev ++;
if (prev == jump)
{
return -1;
}
}
if (arr[prev] == x)
return prev;
return -1;
}Hàm Main
int main(int argc, _TCHAR* argv[])
{
int arr[] = {0, 1, 4, 7, 8, 9, 14, 16, 18, 19, 30, 34, 46, 48, 50, 55, 58};
int s_val = 55;
unsigned int num = sizeof(arr)/sizeof(arr[0]);
int ret1 = JumpSearch(arr, num, s_val);
if (ret1 != -1)
std::cout << "Vi tri cua " << s_val << "la : " << ret1;
else
std::cout << "Khong tim dc";
_getch();
return 0;
}+ Thuật Toán Exponential Search
Bài hôm nay chúng ta cùng tìm hiểu về thuật toán Exponential Search (Thuật toán tìm kiếm theo số mũ)
Nguyên lý Exponential Search
+ Cũng yêu cầu dãy số đầu vào là một dãy đã được xắp xếp cho sẵn.
+ Kết hợp với việc tìm kiếm theo kiểu nhị phân.
+ Tìm ra khoảng con chứa giá trị cần tìm kiếm, và sau đó sử dụng tìm kiếm nhị phân cho khoảng con đó.
Độ phức tạp thời gian mà nó đạt được là: Log2(n).
Step 1:
+ Kiểm tra phần tử 0 của tập để xem nó có phải là phần tử tìm kiếm hay không.
+ Nếu không thì bắt đầu giá trị chạy từ 1 và kiểm tra nó < giá trị cần tìm hay không.
=> Nếu có, thì tiếp tục tăng giá trị chạy lên theo công thức : i = i*2;
=> Nếu không, thì chứng tỏ giá trị cần tìm đang năm trong khoảng từ i/2 đến i
Vì a[i] > X và vòng lặp trước đó là a[i/2] < X.
Do đó ta tìm được khoảng con chứa giá trị X cần tìm
Step 2:
Áp dụng Binary Search cho khoảng con vừa tìm được.
Thực hành
// Techacademy.edu.vn
#include <iostream>
#include <conio.h>
int BinarySearch(int arr[], const int&, const int&, const int&);
int ExponentialSearch(int arr[], int n, int x)
{
if (arr[0] == x)
return 0;
int i = 1;
while (i < n && arr[i] <= x)
i = i*2;
return BinarySearch(arr, i/2, std::min(i, n), x);
}
int BinarySearch(int arr[], const int& l, const int& r, const int& x)
{
if (r >= l)
{
int mid = l + (r - l)/2;
if (arr[mid] == x)
return mid;
if (arr[mid] > x)
return BinarySearch(arr, l, mid-1, x);
return BinarySearch(arr, mid+1, r, x);
}
return -1;
}
int main(int argc, _TCHAR* argv[])
{
int arr[] = {1, 3, 6, 7, 9, 11, 14, 33, 36};
int n = sizeof(arr)/ sizeof(arr[0]);
int x = 14;
int ret = ExponentialSearch(arr, n, x);
if (ret == -1)
std::cout << "Khong tim dc";
else
std::cout << "Gia tri can tim tai vi tri: " << ret;
_getch();
return 0;
}+ Phù hợp cho việc tìm kiếm các mảng có số lượng phần tử lớn, hoặc phần từ tìm kiếm nằm gần đầu danh sách, (Nhanh tìm ra tập còn chứa giá trị tìm kiếm).
3. Bài Tập Về Thuật Toán Tìm Kiếm Trong C++
Sau đây là các bước triển khai thuật toán, các bước thực hiện đều được comment ở từng đoạn.
#include <bits/stdc++.h>
using namespace std;
//Hàm tìm kiếm nhi phân
int binarySearch(int arr[], int left, int right, int x) {
int middle;
while(left <= right) {
// Lấy vị trí ở giữa left và right
middle = (left + right) / 2;
// Nếu phần từ ở giữa bằng x thì trả về
// vị trí
if (arr[middle] == x)
return middle;
// Nếu x lớn hơn phần tử ở giữa thì
// chắc chắn nó nằm bên phải.
// Chỉ định left phần từ ở giữa + 1
if (x > arr[middle])
left = middle + 1;
else
//Ngược lại
right = middle - 1;
}
//Trả về -1 nếu không tìm thấy gía trị trong mảng.
return -1;
}
int main() {
int arr[] = {15, 20, 25, 30, 31, 44, 66};
//Lấy ra độ dài của mảng
int n = sizeof(arr) / sizeof(arr[0]);
//Phần từ cần tìm
int x = 25;
// n -1 là vị trí cuối cùng trong mảng.
int result = binarySearch(arr, 0, n-1, x);
cout << result;
}Khởi chạy chươn trình chúng ta sẽ nhận được kết quả là vị trí của 25 trong mảng.
Có nhiều điểm khác biệt và tương đồng giữa ngôn ngữ lập trình C++ và Java . Dưới đây là danh sách những điểm khác Read more
Con trỏ là một trong những tính năng quan trọng của mỗi ngôn ngữ lập trình. Thực tế, để được Read more
Danh sách liên kết đơn là gì? Danh sách đơn liên kết (Danh sách liên kết đơn) là một dữ Read more
Con trỏ và cấp phát động trong C++ Con trỏ (pointer) là một khái niệm quan trọng và khó nhất Read more
Để lại một phản hồi
Bạn phải đăng nhập để gửi phản hồi.